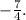Question

F(x) = 1 / 2
g(x) = x - 4
Can you evaluate (g o f) (0)? Explain why or why
not.

Answer 1

Sample Response: To evaluate the composition, you need to find the value of function f first. But, f(0) is 1 over 0, and division by 0 is undefined. Therefore, you cannot find the value of the composition.

What did you include in your answer?

You must evaluate the function f first.

Division by 0 is undefined.

The composition cannot be evaluated.

Answer 2

For this case we have the following functions:

`f (x) = \frac {1} {2}\\g (x) = x-4`

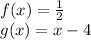
We must find
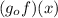`(g_ {o} f) (x)`. For definition of composition of functions we have to:

`(g_ {o} f) (x) = g (f (x))`

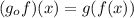
So:

`g (f (x)) = \frac {1} {2} -4 = \frac {1-8} {4} = \frac {-7} {4} = - \frac {7} {4}`

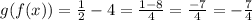
Then, for any value of "x", the composite function has a value of
`- \frac {7} {4}`.

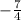Thus,
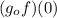`(g_ {o} f) (0)`cannot be evaluated, it will always be obtained
`- \frac {7} {4}.`

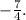
ANswer:

For any value of "x", the composite function has a value of
`- \frac {7} {4}.`