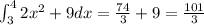Answer:
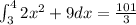
Explanation:
The Fundamental Theorem of Calculus says,
Suppose
 is a continuous function on
is a continuous function on
![[a,b]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/x9eybysx3cihgn4xxsxk4fl3z5dcnyp7ww.png) and also suppose that
and also suppose that
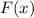 is any anti-derivative for
is any anti-derivative for

Using the above definition, we can evaluate the definite integral
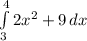
First,

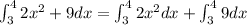
Evaluate the integral
![\int _3^42x^2dx=2\cdot \int _3^4x^2dx\\\\\mathrm{Apply\:the\:Power\:Rule}:\quad \int x^adx=(x^(a+1))/(a+1),\:\quad \:a\\e -1\\\\2\left[(x^(2+1))/(2+1)\right]^4_3=2\left[(x^3)/(3)\right]^4_3\\\\\mathrm{Compute\:the\:boundaries}:\\\\2((4^3)/(3)-(3^3)/(3)) =2\cdot (37)/(3)= (74)/(3)](https://img.qammunity.org/2020/formulas/mathematics/college/r2d6ses48k8pl1ezskhqqwe0zu5pz3ie72.png)
and the integral
![\int _3^49dx=\left[9x\right]^4_3=9(4)-9(3)=9](https://img.qammunity.org/2020/formulas/mathematics/college/6inh407un0q1ghi1pjiw4u86or3f601f43.png)
Finally, we get that