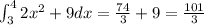Question

Use the fundamental theorem of calculus to evaluate the following definite integral. Integral from 3 to 4 (2 x squared plus 9 )dx∫342x2+9 dx Integral from 3 to 4 (2 x squared plus 9 )dx∫342x2+9 dx

Answer 1

`\int _3^42x^2+9dx=(101)/(3)`

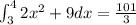
Explanation:

The Fundamental Theorem of Calculus says,

Suppose
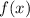`f(x)` is a continuous function on
`[a,b]` and also suppose that
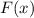`F(x)` is any anti-derivative for

`\int_{{\,a}}^{{\,b}}{{f\left( x \right)dx}} = \left. {F\left( x \right)} \right|_a^b = F\left( b \right) - F\left( a \right)`

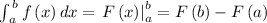
Using the above definition, we can evaluate the definite integral
`\int\limits^4_3 {2x^2+9} \, dx`

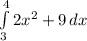
First,

`\mathrm{Apply\:the\:Sum\:Rule}:\quad \int f\left(x\right)\pm g\left(x\right)dx=\int f\left(x\right)dx\pm \int g\left(x\right)dx`

`\int _3^42x^2+9dx=\int _3^42x^2dx+\int _3^49dx`

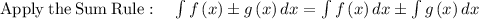
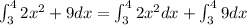
Evaluate the integral

`\int _3^42x^2dx=2\cdot \int _3^4x^2dx\\\\\mathrm{Apply\:the\:Power\:Rule}:\quad \int x^adx=(x^(a+1))/(a+1),\:\quad \:a\\e -1\\\\2\left[(x^(2+1))/(2+1)\right]^4_3=2\left[(x^3)/(3)\right]^4_3\\\\\mathrm{Compute\:the\:boundaries}:\\\\2((4^3)/(3)-(3^3)/(3)) =2\cdot (37)/(3)= (74)/(3)`

and the integral

`\int _3^49dx=\left[9x\right]^4_3=9(4)-9(3)=9`

Finally, we get that

`\int _3^42x^2+9dx=(74)/(3)+9=(101)/(3)`

Answer 2

Theorem of calculus

Explanation:

Take the integral

`\int\limits^3_4 (2x^2+9)dx`

Integrate the sum term by term and factor out constants

`= 2 \int\limits^4_3 x^2 dx + 9 \int\limits^4_3 1 dx`

Apply the fundamental theorem of calculus.

The antiderivative of x^2 is x^3/3, while for a constat is x

`= (2x^3)/(3) + 9x dx`

Evaluate the limits

`= (2*((4)^3)/(3)+9*4)-(2*((3)^3)/(3)+9*3)`

`=(101)/(3)`