Answer:
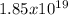 attempts are required to find a matching pair if the digital fingerprint is 64 bits long.
attempts are required to find a matching pair if the digital fingerprint is 64 bits long.
 attempts are required to find a matching pair if the digital fingerprint is 128 bits long.
attempts are required to find a matching pair if the digital fingerprint is 128 bits long.
Explanation:
Each bit has two options. So
How many attempts are required to find a matching pair if the digital fingerprint is 64 bits long?
So for each of the 64 bits, we have the following number of options.
2 - 2 - 2 - 2 -... - 2
So, in all, there are
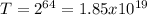
options.
So,
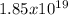 attempts are required to find a matching pair if the digital fingerprint is 64 bits long.
attempts are required to find a matching pair if the digital fingerprint is 64 bits long.
128 bits long?
Using the same logic as the first question.
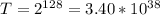
So,
 attempts are required to find a matching pair if the digital fingerprint is 128 bits long.
attempts are required to find a matching pair if the digital fingerprint is 128 bits long.