Answer:
If only slope:
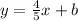
If slope and y-intercept:
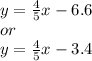
*both are correct answers see steps below*
Explanation:
The equation to find the slope is
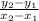 .
.
The equation for slope-intercept form is
 .
.
First, find the slope between two points.
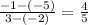
Keep the difference as a fraction if it can't be divided.
Next, plug in the slope value into the equation.
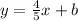
If you also need to find what b is, pick a point; (-2, -5) OR (3, -1). Then fill in the equation with it's x and y values. (I'll do both points to show two different results).
Point (-2, -5):
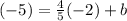
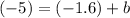
Add 1.6 on both sides to isolate the b. (since -1.6 is a negative, we need to cancel it out with its opposite)

Point (3, -1):
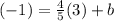
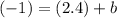
Subtract 2.4 on both sides to isolate the b. (since 2.4 is a positive, we need to cancel it out with its opposite)

It does mean that both slopes have different y-intercepts but it overly depends on the point. These steps will ensure you to the correct answer.