Question

A power washer is being used to clean the siding of a house. Water enters at 20 C, 1 atm, with a volumetric flow rate of 0.1 liter/s through a 2.5-cm-diameter hose. A jet of water exits at 23 C, 1 atm, with a velocity of 50 m/s at an elevation of 5 m. At steady state, the magnitude of the heat transfer rate from the power unit to the surroundings is 10% of the power input. Determine the power input to the motor, kW.

Answer 1

W=1259W=1.2Kw

Step-by-step explanation:

Hello!

The first step to solve is to find the enthalpies at the entrance (state 1) and the exit of the washer, for this we use the thermodynamic tables.

Through laboratory tests, thermodynamic tables were developed, these allow to know all the thermodynamic properties of a substance (entropy, enthalpy, pressure, specific volume, internal energy etc ..)

through prior knowledge of two other properties such as pressure and temperature.

state 1

h1(T=20C,P=1atm)=83.93kJ/kg

state 2

h1(T=23C,P=1atm)=96.48kJ/kg

now we find the mass flow remembering that it is the product of the flow rate by the density=

m= mass flow

`M=\alpha q`

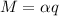
q=flow=0.1l/S=0.0001M^3/s

α=Density=1000kg/m^3

m=0.1kg/s

Now we draw the energy flows in the washer (see attached image) and propose the first law of thermodynamics that states that the energy that enters must be equal to the one that comes out

`mh1+W+(v1^2)/(2g) =0.1W+mh2+(v2^2)/(2g)+mgH`

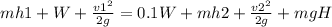
where

m=mass flow

h=entalpy

v=speed

W=power input

g=gravity

H=height

SOLVING FOR W

`W=(m2h2-m1h1+m(v2^2-v1^2)/(g)+mgH)/(1.1)`

`W=((0.1)(96480)-(0.1)(83930)+(0.1(50^2-0.2^2))/(2)+0.1(9.81)(5))/(1.1)`

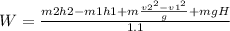
W=1259W=1.2Kw