Answer:
This process is not adiabatic.
Direction: System to surrounding.
Step-by-step explanation:
The change of entropy is:
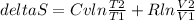
Replacing:
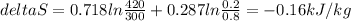
As seen in the result, entropy is negative, therefore, the system is losing heat. Therefore, this process is not adiabatic.
The direction of heat transfer is:
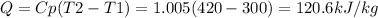
Direction: System to surrounding.