Question

A chemist has three different acid solutions. The first acid solution contains 20 % acid, the second contains 35 % and the third contains 75 % . He wants to use all three solutions to obtain a mixture of 45 liters containing 60 % acid, using 3 times as much of the 75 % solution as the 35 % solution. How many liters of each solution should be used?

Answer 1

5 L , 10 L and 30 L of each solution should be used respectively.

Step-by-step explanation:

Volume of solution-1 = x

Volume of solution-2 = y

Volume of solution-3 = z

Total volume of an acid solution desired = 45 L

x + y + z = 45 L

Percentage of an acid in solution-1 = 20%

Volume of an acid in solution-1 = 20% of x = 0.2x

Percentage of an acid in solution-2 = 35%

Volume of an acid in solution-2 = 35% of y = 0.35y

Percentage of an acid in solution-3 = 75%

Volume of an acid in solution-3 = 75% of z = 0.75z

Percentage of an acid solution desired = 60%

Volume of an acid in desired solution =
`(60)/(100)* 45 L=27L`

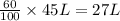
Sum of volume of acids in all three solution will be equal to 27 L.

0.2x + 0.35y + 0.75z = 27 L

Also give that, chemist want prepare solution by using 3 times as much of the 75 % solution as the 35 % solution.

3y = z

x + y + z = 45 L

x + 4y = 45 L..[1]

0.2x + 0.35y + 0.75z = 27 L

0.2x + 0.35y + 0.75(3y) = 27 L

0.2x + 2.6y= 27 L...[2]

On solving [1] and [2] ,we get:

x = 5 L

y = 10 L

z = 3y = 30 L

5 L , 10 L and 30 L liters of each solution should be used respectively.