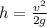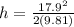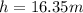Question

A skier starts from rest at the top of a hill. The skier coasts down the hill and up a second hill, as the drawing illustrates. The crest of the second hill is circular, with a radius of 32.7 m. Neglect friction and air resistance. What must be the height h of the first hill so that the skier just loses contact with the snow at the crest of the second hill?

Answer 1

`h = 16.35 m`

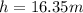
Step-by-step explanation:

Here we have the total energy is conserved so when skier start from first hill and reach the second hill then we can use energy conservation for its motion

initial potential energy = final kinetic energy

so we have

`mgh = (1)/(2)mv^2`

now we know that skier will not lose its contact on second hill so we have

`(mv^2)/(R) = mg`

`v^2 = Rg`

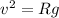
now we have

R = 32.7 m

`v^2 = 32.7 * 9.8`

`v = 17.9 m/s`

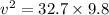
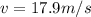
now from above equation we have

`mgh = (1)/(2)mv^2`

`h = (v^2)/(2g)`

`h = (17.9^2)/(2(9.81))`

`h = 16.35 m`