Answer:
Part a) The volume of the original pyramid is
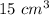
Part b) The volume of the pyramid increases by
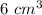
Explanation:
The complete question is
Part 1) The volume of the pyramid shown in the figure is 9,15,21, or 63 cubic centimeters?. Part 2) If the slant height of the pyramid increases by 4 centimeters and its height increases by 2 centimeters, the volume of the pyramid increases by 6,9,12 or 21 cubic centimeters?
we know that
The volume of the pyramid is equal to

where
B is the area of the base
h is the height of pyramid
see the attached figure to better understand the problem
Step 1
Find the volume of the original pyramid
the area of the base B is equal to

substitute
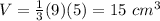
Step 2
Find the volume of the new pyramid
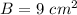 -------> the area of the base is the same
-------> the area of the base is the same
 ------> the height increase by
------> the height increase by
substitute
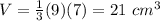
Subtract the original volume from the new volume
