Answer:
Lilly's speed is two times John's speed.
Step-by-step explanation:
m = Mass
a = Acceleration
t = Time taken
u = Initial velocity
v = Final velocity
The force they apply on each other will be equal
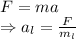
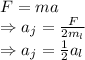
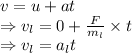
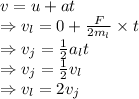
Hence, Lilly's speed is two times John's speed.