Question

Two ice skaters, Lilly and John, face each other while at rest, and then push against each other's hands. The mass of John is twice that of Lilly. How do their speeds compare after they push off? Lilly's speed is one-fourth of John's speed. Lilly's speed is the same as John's speed. Lilly's speed is two times John's speed. Lilly's speed is four times John's speed. Lilly's speed is one-half of John's speed.

Answer 1

Lilly's speed is 2 times Johns speed

Step-by-step explanation:

Answer 2

Lilly's speed is two times John's speed.

Step-by-step explanation:

m = Mass

a = Acceleration

t = Time taken

u = Initial velocity

v = Final velocity

The force they apply on each other will be equal

`F=ma\\\Rightarrow a_l=(F)/(m_l)`

`F=ma\\\Rightarrow a_j=(F)/(2m_l)\\\Rightarrow a_j=(1)/(2)a_l`

`v=u+at\\\Rightarrow v_l=0+(F)/(m_l)* t\\\Rightarrow v_l=a_lt`

`v=u+at\\\Rightarrow v_l=0+(F)/(2m_l)* t\\\Rightarrow v_j=(1)/(2)a_lt\\\Rightarrow v_j=(1)/(2)v_l\\\Rightarrow v_l=2v_j`

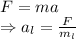
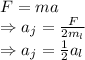
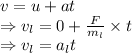
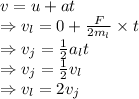
Hence, Lilly's speed is two times John's speed.