Answer:
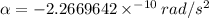
Step-by-step explanation:
Angular acceleration is defined by
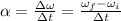
Angular velocity is related to the period by
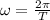
Putting all together:
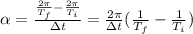
Taking our initial (i) point now and our final (f) point one year later, we would have:
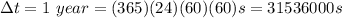
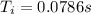
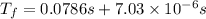
So for our values we have:
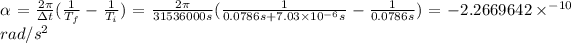
Where the minus sign indicates it is decelerating.