Question

A pulsar is a rapidly rotating neutron star that emits a radio beam the way a lighthouse emits a light beam. We receive a radio pulse for each rotation of the star. The period T of rotation is found by measuring the time between pulses. Suppose a pulsar has a period of rotation of T = 0.0786 s that is increasing at the rate of 7.03 x 10-6 s/y. (a) What is the pulsar's angular acceleration α

Answer 1

`\alpha =-2.2669642*^(-10)rad/s^2`

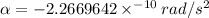
Step-by-step explanation:

Angular acceleration is defined by
`\alpha =(\Delta \omega)/(\Delta t)=(\omega_f-\omega_i)/(\Delta t)`

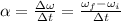
Angular velocity is related to the period by
`\omega=(2\pi)/(T)`

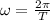
Putting all together:

`\alpha =((2\pi)/(T_f)-(2\pi)/(T_i))/(\Delta t)=(2\pi)/(\Delta t)((1)/(T_f)-(1)/(T_i))`

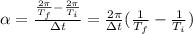
Taking our initial (i) point now and our final (f) point one year later, we would have:

`\Delta t=1\ year=(365)(24)(60)(60)s=31536000 s`

`T_i=0.0786s`

`T_f=0.0786s+7.03*10^(-6)s`

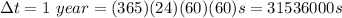
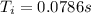
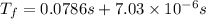
So for our values we have:

`\alpha =(2\pi)/(\Delta t)((1)/(T_f)-(1)/(T_i))=(2\pi)/(31536000s)((1)/(0.0786s+7.03*10^(-6)s)-(1)/(0.0786s))=-2.2669642*^(-10)rad/s^2`

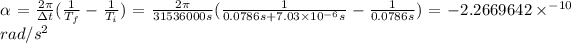
Where the minus sign indicates it is decelerating.