Question

In a right triangle, angle A measures 20°. The side opposite angle A is 10 centimeters long. Approximately how long is the hypotenuse of the triangle?

Answer 1

The hypotenuse of the triangle is 29.23 cm long

Solution:

Given that In a right triangle, angle A measures
`20^(\circ)`

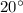
The side opposite angle A is 10 centimeters long

Let a right triangle ABC having right angled at B

According to question, angle A is
`20^(\circ)`

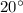
We know by angle sum property of triangle, the sum of all the angles of the triangle is 180 degree

`\begin{array}{l}{A^(\circ)+B^(\circ)+C^(\circ)=180^(\circ)} \\\\ {20^(\circ)+90^(\circ)+C^(\circ)=180^(\circ)} \\\\ {C^(\circ)=180^(\circ)-110^(\circ)} \\\\ {C^(\circ)=70^(\circ)}\end{array}`

`\text { We know } \sin \theta=\frac{\text { Perpendicular }}{\text { Hypotenuse }}`

`\begin{array}{l}{\sin A^(\circ)=(B C) /(A C)} \\\\ {\sin 20^(\circ)=(10) /(A C)} \\\\ {0.342=10 / A C} \\\\ {A C=10 /(0.342)} \\\\ {A C=29.23 \mathrm{cm}}\end{array}`

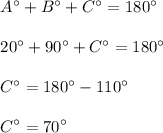
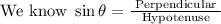
So, the hypotenuse is 29.23 cm long

Answer 2

sin(x) is equal to opposite over hypotenuse, so you can set it up as

sin(20) = 10/x

x = 10/sin(20)

x = 29.2 cm

Explanation: