The hypotenuse of the triangle is 29.23 cm long
Solution:
Given that In a right triangle, angle A measures
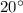
The side opposite angle A is 10 centimeters long
Let a right triangle ABC having right angled at B
According to question, angle A is
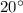
We know by angle sum property of triangle, the sum of all the angles of the triangle is 180 degree
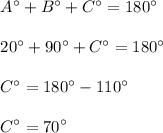
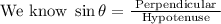

So, the hypotenuse is 29.23 cm long