Answer:
∠C = 37° ,
AB = 26.54 cm ,
BC= 33.27 cm
Explanation:
Given that in triangle ABC
∠A = 39° AC = 20 cm
∠B = 104°
∵ sum of all the three angles of triangle = 180°
So, ∠C = 180° - ( ∠A + ∠B)
∠C = 180° - (39° + 104°)
∠C = 37°
Now Tan 37° =
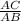
Or, AB =
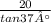
So, AB = 26.54 cm
Again, Sin 37° =
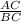
So, BC =
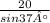
Or, BC =
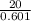
∴ BC= 33.27 cm
Hence ∠C = 37° , AB = 26.54 cm , BC= 33.27 cm Answer