Question

A playground merry-go-round has radius 2.10m and moment of inertia 2500kg*m^2 about a vertical axle through its center, and it turns with negligible friction.

A)A child applies an 18.0 N force tangentially to the edge of the merry-go-round for 16.0s . If the merry-go-round is initially at rest, what is its angular speed after this 16.0s interval?


in rad/s

B)How much work did the child do on the merry-go-round?



C)What is the average power supplied by the child?


I understand the jist of the question but am stuck on where to start

Answer 1

Radius of the wheel r = 2.1 m

Moment of inertia I = 2500 Kg m²

Tangential force applied F = 18 N

Time interval t = 16 s

Initial angular speed ω1 = 0

Final angular speed ω2 = ?

Let α be the angular acceleration.

Torque applied τ = Iα

F r = Iα

Angular acceleration α = F r/I

=
`(18* 2.1)/(2500)`

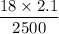
= 0.015 rad/s²

(a)From rotational kinematic relation

Final angular speed ω₂ = ω₁ + αt

= 0 + (0.015 rad/s^2 * 16 s)

= 0.24 rad/s

(b) Work done W = 0.5 Iω₂² - (1/2)Iω₁²

= 0.5*( 2500 Kg m²)(0.24 rad/s)^2 - 0

= 72 J

(c) Average power supplied by the child P = W/t =
`(72)/(16)`

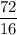
= 4.5 watt