Answer
Radius of the wheel r = 2.1 m
Moment of inertia I = 2500 Kg m²
Tangential force applied F = 18 N
Time interval t = 16 s
Initial angular speed ω1 = 0
Final angular speed ω2 = ?
Let α be the angular acceleration.
Torque applied τ = Iα
F r = Iα
Angular acceleration α = F r/I
=
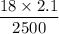
= 0.015 rad/s²
(a)From rotational kinematic relation
Final angular speed ω₂ = ω₁ + αt
= 0 + (0.015 rad/s^2 * 16 s)
= 0.24 rad/s
(b) Work done W = 0.5 Iω₂² - (1/2)Iω₁²
= 0.5*( 2500 Kg m²)(0.24 rad/s)^2 - 0
= 72 J
(c) Average power supplied by the child P = W/t =
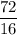
= 4.5 watt