Answer:
Yes, it is, we need to use the Moivre theorem and we get
Explanation:
Hi, first, let´s introduce Moivre theorem to find the nth power of a complex number.
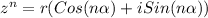
Where:
r = module of the complex number
n= power
alpha= inclination angle
to find the module of the complex number, we need to use the following formula.
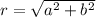
Where:
z= a+bi
a= real part of the coplex number
b=imaginary part of the complex number
Finally, in order to find the angle (alpha), we have to use the following.
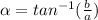
But, using Moivre for a complex number to the 20th power is not very practical, so we are going to assume some things first
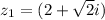

So, first we are going to find the value of
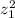 and elevate it to the 10th power in order to get
and elevate it to the 10th power in order to get
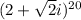
First, lets find the module of z1

and its angle is:
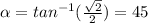
we are all set, now let´s find the value of z_{1} ^{2}
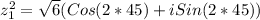
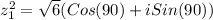 }
}
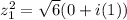
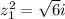
Now, let´s find the value of

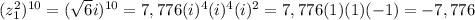
therefore:
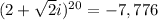
We do the same for (2 − √2i)^20, this time:
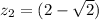

And the angle is
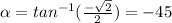
Therefore, we get:
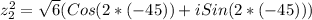

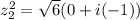
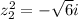
Now, let´s find the value of
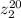
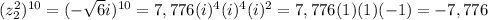
therefore:
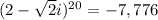
And then, we add them up
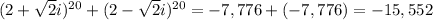
So, yes, the result is an integer, -15,552