Question

Show that (2 + √2i)^20+ (2 − √2i)^20is an integer.

Answer 1

Yes, it is, we need to use the Moivre theorem and we get

Explanation:

Hi, first, let´s introduce Moivre theorem to find the nth power of a complex number.

`z^(n) =r(Cos(n\alpha )+iSin(n\alpha ))`

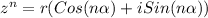
Where:

r = module of the complex number

n= power

alpha= inclination angle

to find the module of the complex number, we need to use the following formula.

`r=\sqrt{a^(2) +b^(2) }`

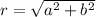
Where:

z= a+bi

a= real part of the coplex number

b=imaginary part of the complex number

Finally, in order to find the angle (alpha), we have to use the following.

`\alpha =tan^(-1) ((b)/(a) )`

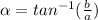
But, using Moivre for a complex number to the 20th power is not very practical, so we are going to assume some things first

`z_(1) =(2+√(2) i)`

`z_(2) =(2-√(2) i)`

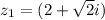
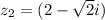
So, first we are going to find the value of
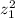`z_(1) ^(2)` and elevate it to the 10th power in order to get
`(2+√(2) i)^(20)`

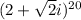
First, lets find the module of z1

`r_(1) =\sqrt{2^(2) +(√(2) )^(2) }=√(4+2) =√(6)`

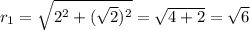
and its angle is:

`\alpha =tan^(-1) ((√(2) )/(2) )=45`

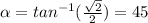
we are all set, now let´s find the value of z_{1} ^{2}

`z_(1) ^(2) =√(6) (Cos(2*45 )+iSin(2*45 ))`

`z_(1) ^(2) =√(6) (Cos(90 )+iSin(90 ))`}

`z_(1) ^(2) =√(6) (0+i(1))`

`z_(1) ^(2)=√(6) i`

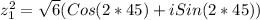
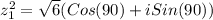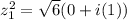
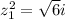
Now, let´s find the value of
`z_(1) ^(20)`

`(z_(1) ^(2))^(10) =(√(6) i)^(10) =7,776(i)^(4) (i)^(4) (i)^(2) =7,776(1)(1)(-1)=-7,776`

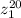
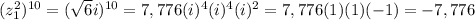
therefore:

`(2 + √(2) i)^(20) =-7,776`

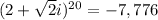
We do the same for (2 − √2i)^20, this time:

`z_(2) =(2-√(2))`

`r_(2) =\sqrt{2^(2) +(-√(2) )^(2) }=√(4+2) =√(6)`

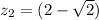
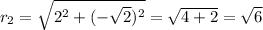
And the angle is

`\alpha =tan^(-1) ((-√(2) )/(2) )=-45`

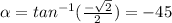
Therefore, we get:

`z_(2) ^(2) =√(6) (Cos(2*(-45) )+iSin(2*(-45) ))`

`z_(2) ^(2) =√(6) (Cos(-90 )+iSin(-90 ))`

`z_(2) ^(2) =√(6) (0+i(-1))`

`z_(2) ^(2)=-√(6) i`

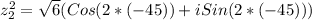
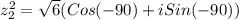
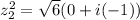
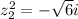
Now, let´s find the value of
`z_(2) ^(20)`

`(z_(2) ^(2))^(10) =(-√(6) i)^(10) =7,776(i)^(4) (i)^(4) (i)^(2) =7,776(1)(1)(-1)=-7,776`

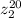
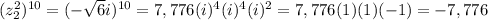
therefore:

`(2 - √(2) i)^(20) =-7,776`

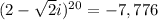
And then, we add them up

`(2+√(2) i)^(20)+(2-√(2) i)^(20)=-7,776+(-7,776)=-15,552`

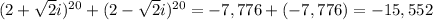
So, yes, the result is an integer, -15,552