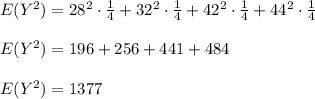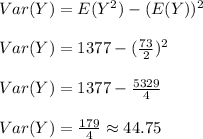Question

Four buses carrying 146 high school students arrive to Montreal. The buses carry, respectively, 32, 44, 28, and 42 students. One of the studetns is randomly selected. Let X denote the number of students that were on the bus carrying this randomly selected student. One of the 4 bus drivers is also randomly selected. Let Y denote the number of students on his bus. Compute the expectations and variances of X and Y

Answer 1

The expected value of X is
`E(X)=(2754)/(73) \approx 37.73` and the variance of X is
`Var(X)=(226192)/(5329) \approx 42.45`

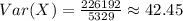
The expected value of Y is
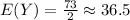`E(Y)=(73)/(2) \approx 36.5` and the variance of Y is
`Var(Y)=(179)/(4) \approx 44.75`

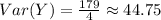
Explanation:

(a) Let X be a discrete random variable with set of possible values D and probability mass function p(x). The expected value, denoted by E(X) or
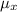`\mu_x`, is

`E(X)=\sum_(x\in D) x\cdot p(x)`

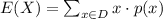
The probability mass function
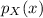`p_(X)(x)` of X is given by

`p_(X)(28)=(28)/(146) \\\\p_(X)(32)=(32)/(146) \\\\p_(X)(42)=(42)/(146) \\\\p_(X)(44)=(44)/(146)`

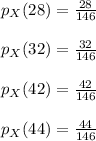
Since the bus driver is equally likely to drive any of the 4 buses, the probability mass function
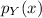`p_(Y)(x)` of Y is given by

`p_(Y)(28)=p_(Y)(32)=p_(Y)(42)=p_(Y)(44)=(1)/(4)`

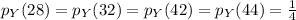
The expected value of X is

`E(X)=\sum_(x\in [28,32,42,44]) x\cdot p_(X)(x)`

`E(X)=28\cdot (28)/(146)+32\cdot (32)/(146) +42\cdot (42)/(146) +44 \cdot (44)/(146)\\\\E(X)=(392)/(73)+(512)/(73)+(882)/(73)+(968)/(73)\\\\E(X)=(2754)/(73) \approx 37.73`

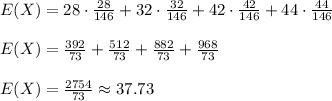
The expected value of Y is

`E(Y)=\sum_(x\in [28,32,42,44]) x\cdot p_(Y)(x)`

`E(Y)=28\cdot (1)/(4)+32\cdot (1)/(4) +42\cdot (1)/(4) +44 \cdot (1)/(4)\\\\E(Y)=146\cdot (1)/(4)\\\\E(Y)=(73)/(2) \approx 36.5`

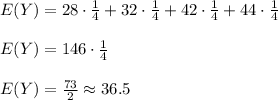
(b) Let X have probability mass function p(x) and expected value E(X). Then the variance of X, denoted by V(X), is

`V(X)=\sum_(x\in D) (x-\mu)^2\cdot p(x)=E(X^2)-[E(X)]^2`

The variance of X is

`E(X^2)=\sum_(x\in [28,32,42,44]) x^2\cdot p_(X)(x)`

`E(X^2)=28^2\cdot (28)/(146)+32^2\cdot (32)/(146) +42^2\cdot (42)/(146) +44^2 \cdot (44)/(146)\\\\E(X^2)=(10976)/(73)+(16384)/(73)+(37044)/(73)+(42592)/(73)\\\\E(X^2)=(106996)/(73)`

`Var(X)=E(X^2)-(E(X))^2\\\\Var(X)=(106996)/(73)-((2754)/(73))^2\\\\Var(X)=(106996)/(73)-(7584516)/(5329)\\\\Var(X)=(7810708)/(5329)-(7584516)/(5329)\\\\Var(X)=(226192)/(5329) \approx 42.45`

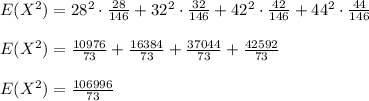
The variance of Y is

`E(Y^2)=\sum_(x\in [28,32,42,44]) x^2\cdot p_(Y)(x)`

`E(Y^2)=28^2\cdot (1)/(4)+32^2\cdot (1)/(4) +42^2\cdot (1)/(4) +44^2 \cdot (1)/(4)\\\\E(Y^2)=196+256+441+484\\\\E(Y^2)=1377`

`Var(Y)=E(Y^2)-(E(Y))^2\\\\Var(Y)=1377-((73)/(2))^2\\\\Var(Y)=1377-(5329)/(4)\\\\Var(Y)=(179)/(4) \approx 44.75`