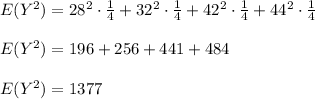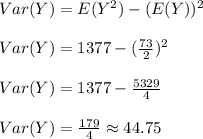Answer:
The expected value of X is
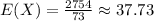 and the variance of X is
and the variance of X is
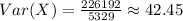
The expected value of Y is
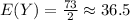 and the variance of Y is
and the variance of Y is
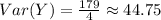
Explanation:
(a) Let X be a discrete random variable with set of possible values D and probability mass function p(x). The expected value, denoted by E(X) or
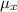 , is
, is
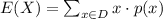
The probability mass function
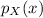 of X is given by
of X is given by
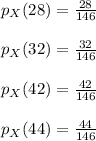
Since the bus driver is equally likely to drive any of the 4 buses, the probability mass function
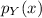 of Y is given by
of Y is given by
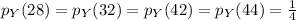
The expected value of X is
![E(X)=\sum_(x\in [28,32,42,44]) x\cdot p_(X)(x)](https://img.qammunity.org/2020/formulas/mathematics/college/28s05mx98mw0266vh2k43sk13eqursjnqs.png)
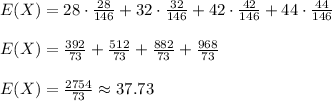
The expected value of Y is
![E(Y)=\sum_(x\in [28,32,42,44]) x\cdot p_(Y)(x)](https://img.qammunity.org/2020/formulas/mathematics/college/ccaiivzpu187zkxc7hau1nn8cw44s8zdxl.png)
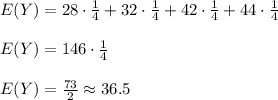
(b) Let X have probability mass function p(x) and expected value E(X). Then the variance of X, denoted by V(X), is
![V(X)=\sum_(x\in D) (x-\mu)^2\cdot p(x)=E(X^2)-[E(X)]^2](https://img.qammunity.org/2020/formulas/mathematics/college/sfs4rp7ovauluc6umlpbuu7onn4etb4uwa.png)
The variance of X is
![E(X^2)=\sum_(x\in [28,32,42,44]) x^2\cdot p_(X)(x)](https://img.qammunity.org/2020/formulas/mathematics/college/4j22mpe0oqfcbgkq465u0hzauezz51sw39.png)
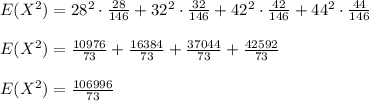
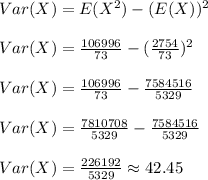
The variance of Y is
![E(Y^2)=\sum_(x\in [28,32,42,44]) x^2\cdot p_(Y)(x)](https://img.qammunity.org/2020/formulas/mathematics/college/1itxa452b7te461g813p4hcmq41ieaooo5.png)