Question

Which of the following is the simplified form of fifth root of x times the fifth root of x times the fifth root of x times the fifth root of x?

Answer 1

x^4/5

Explanation:

Answer 2

Simplified form of fifth root of x times the fifth root of x times the fifth root of x times the fifth root of x is
`\sqrt[5]{x^(4)}`

Solution:

Need to find simplified form of fifth root of x times the fifth root of x times the fifth root of x times the fifth root of x. That is need to find simplified form of following expression.

`\sqrt[5]{x} * \sqrt[5]{x} * \sqrt[5]{x} * \sqrt[5]{x}`

`\text { since } \sqrt[n]{a}=(a)^{(1)/(n)}` we get

`=>(x)^{(1)/(5)} *(x)^{(1)/(5)} *(x)^{(1)/(5)} *(x)^{(1)/(5)}`

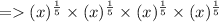
Now using law of exponent that is
`\mathrm{a}^{\mathrm{m}} * \mathrm{a}^{\mathrm{n}}=\mathrm{a}^{\mathrm{m}+\mathrm{n}}`

`\begin{array}{l}{\Rightarrow(x)^{(1)/(5)} *(x)^{(1)/(5)} *(x)^{(1)/(5)} *(x)^{(1)/(5)}} \\\\ {=(x)^{(1)/(5)+(1)/(5)} *(x)^{(1)/(5)}} \\\\ {=(x)^{(2)/(5)} *(x)^{(2)/(5)}} \\\\ {=(x)^{(2)/(5)} *(x)^{(2)/(5)}} \\\\ {=(x)^{(2)/(5) +(2)/(5) \\\\ {=(x)^{(4)/(5)}}\end{array}`

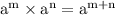
Using another law of exponent that is
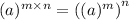`(a)^(m * n)=\left((a)^(m)\right)^(n)` we get

`\begin{array}{l}{(x)^{(4)/(5)}=(x)^{4 * (1)/(5)}=\left((x)^(4)\right)^{(1)/(5)}} \\\\ {\left((x)^(4)\right)^{(1)/(5)}=\sqrt[5]{x^(4)}}\end{array}`

Hence the simplified form of fifth root of x times the fifth root of x times the fifth root of x times the fifth root of x is
`\sqrt[5]{x^(4)}`