Question

The function f(x) varies directly with x, and f(x) = 45 when x = 9.

Evaluate f(x) when x= 3.

A=5
B=9
C=15
D=27

Answer 1

Option C = 15

Explanation:

In principle when a function f(x) varies directly with x it suggests that any changes in x results in the equivalent changes in f(x). If we have two variables, i.e. y representing f(x) and x representing itself, any increment/decrement in x will result to the same increment/decrement in y by a factor a, thus we can say that y = ax, implying y and x have the same ratio.

In the given question we know that
`f(x) = 45` when
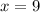`x=9`, which translates as

`f(x=9) = 45`

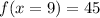
This tells us that
`f(x)` varies by a factor (lets call it)
`a` for a given value of
`x`.

To find this factor we can just divide 45 with 9 which gives:
`(45)/(9) = 5`

Thus the factor
`a` here is
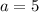`a=5` which finally tells us that

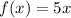`f(x) = 5x` Eqn (1) our original function.

Since we now know our function we can plug in the value for
`x=3` and solve for
`f(x=3)` as follow:

`f(x=3)= 5*3`

`f(x=3) = 15`

`f(3) = 15`

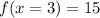
Looking at the given options in the question we can conclude that the correct answer is Option C = 15