Answer:
a. A = -1 and B = 1
b. A = 7 and B = -5
Explanation:
a.
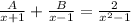
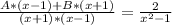
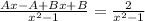
To the equation be true, the "x-parts" and "nonx-parts" mist be the same, so:
Ax + Bx = 0
(A + B)x = 0
A + B = 0
A = -B
B - A = 2
B - (-B) = 2
2B = 2
B = 1 and A = -1
b.
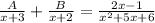
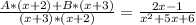
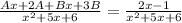
To the equation be true, the "x-parts" and "nonx-parts" mist be the same, so:
Ax + Bx = 2x
(A + B)x = 2x
A + B = 2
A = 2 - B
2A + 3B = -1
2*(2-B) + 3B = -1
4 - 2B + 3B = -1
B = -5 and A = 2 - (-5) = 7