Question

A vector has a x component of -25 units and y component of 40 units find the magnitude and direction

Answer 1

47.2 units at
`122^(\circ)`

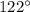
Step-by-step explanation:

The components of the vector are:

x = -25

y = 40

The two components form the sides of a right triangle, of which the vector itself represents the hypothenuse; therefore, we can find the magnitude of the vector by using the Pythagorean theorem:

`v=√(x^2+y^2)=√((-25)^2+(40)^2)=47.2`

Concerning the direction, we can apply the formula:

`\theta =tan^(-1) ((y)/(|x|)) = tan^(-1)((40)/(25))=58.0^(\circ)`

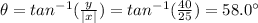
The x-component is, however, negative, so the correct angle (measured anticlockwise from the positive x-axis) is

`\theta = 180 -58 = 122^(\circ)`