Question

The sodium content of twenty 300-gram boxes of organic cornflakes was determined. The data (in milligrams) are as follows: 131.15, 130.69, 130.91, 129.54, 129.64, 128.77, 130.72, 128.33, 128.24, 129.65, 130.14, 129.29, 128.71, 129.00, 129.39, 130.42, 129.53, 130.12, 129.78, 130.92 In this question, we want to verify whether the true mean sodium content of this brand of cornflakes differs from 130 milligrams under the significance level, a = 0.05.

Answer 1

The content of the brand actually differs from the expected average with the specified significance.

Step-by-step explanation:

Hello,

By considering the given data, the average is computed via the addition of all the data divided by the sample's size:

`m_(Na)=(sum(m_i))/(20)`

`m_(Na)=(2594.94mg)/(20) =129.747mg`

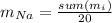
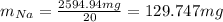
Now, that result, based on the significance, is compared with the following result:

`130-0.05=129.95mg`

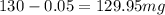
Since the computed average is less than the previous result containing the significance, one states that the content of the brand actually differs from the expected average with the specified significance.

Best regards.