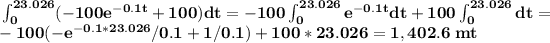Question

The rate of change of the downward velocity of a falling object is the acceleration of gravity (10 meters/sec 2) minus the acceleration due to air resistance. Suppose that the acceleration due to air resistance is 0.1 inverse seconds times the downward velocity. Write the initial value problem and the solution for the downward velocity for an object that is dropped (not thrown) from a great height. dv -10-0.1v y(t)-| 10-10e-0.1 x what is the terminal velocity?meters/second How long before the object reaches 90% of terminal velocity? How far has it fallen by that time? seconds ,namwww.janv. Progr?? .Practoe Another venion

Answer 1

See below

Explanation:

Write the initial value problem and the solution for the downward velocity for an object that is dropped (not thrown) from a great height.

if v(t) is the speed at time t after being dropped, v'(t) is the acceleration at time t, so the the initial value problem for the downward velocity is

v'(t) = 10 - 0.1v(t)

v(0) = 0 (since the object is dropped)

The equation v'(t)+0.1v(t)=10 is an ordinary first order differential equation with an integrating factor

`\bf e^{\int {0.1dt}}=e^(0.1t)`

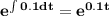
so its general solution is

`\bf v(t)=Ce^(-0.1t)+100`

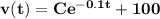
To find C, we use the initial value v(0)=0, so C=-100

and the solution of the initial value problem is

`\bf \boxed{v(t)=-100e^(-0.1t)+100}`

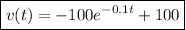
what is the terminal velocity?

The terminal velocity is

`\bf \lim_(t \to\infty)(-100e^(-0.1t)+100)=100\;mt/sec`

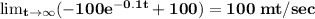
How long before the object reaches 90% of terminal velocity?

90% of terminal velocity = 90 m/sec

we look for a t such that

`\bf -100e^(-0.1t)+100=90\rightarrow -100e^(-0.1t)=-10\rightarrow e^(-0.1t)=0.1\\-0.1t=ln(0.1)\rightarrow t=(ln(0.1))/(-0.1)=23.026\;sec`

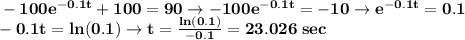
How far has it fallen by that time?

The distance traveled after t seconds is given by

`\bf \int_(0)^(t)v(t)dt`

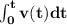
So, the distance traveled after 23.026 seconds is

`\bf \int_(0)^(23.026)(-100e^(-0.1t)+100)dt=-100\int_(0)^(23.026)e^(-0.1t)dt+100\int_(0)^(23.026)dt=\\-100(-e^(-0.1*23.026)/0.1+1/0.1)+100*23.026=1,402.6\;mt`