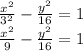Question

Let F(0,5) and ????(0, −5) be the foci of a hyperbola. Let the points P(x, y) on the hyperbola satisfy either

PF − PG = 6 or PG− PF = 6. Use the distance formula to derive an equation for this hyperbola, writing your
answer in the form
x2 / a2 − y2 / b2 = 1.

Answer 1

Explanation:

Remember, the points P on the hyperbola satisfy that the value absolute of the difference of the distances of P to the foci is constant and less than the distance between the foci.

Then

`\lvert\lvert PF\lvert\lvert-\lvert\lvertPG\lvert\lvert=2a, \; \lvert\lvert PG\lvert\lvert-\lvert\lvert PF\lvert\lvert=2a`

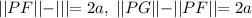
Therefore,
`2a=6\\a=3`

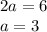
Also, the foci
`(0,c)=(0,5), \; (0,-c)=(0,5)` satisfy that
`c=√(a^2+b^2)`, then

`5=√(3^2+b^2)\\5^2=3^2+b^2\\25-9=b^2\\16=b^2`

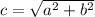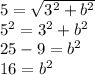
Then, the equaton of the hyperbola is

`(x^2)/(3^2)-(y^2)/(16)=1\\(x^2)/(9)-(y^2)/(16)=1`