Question

What fraction of the radiative flux emitted by the sun is intercepted by Mars (1.52 AU), radius of the planet is 3390 km; compare with the similar number for the earth?

Answer 1

6.9824931E-10

Step-by-step explanation:

Sun's radiative flux can be expressed as a function of Sun's radius and distance from its center:

`\alpha ((R_(Sun))/(r))^2`

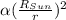
where
`\alpha` is the heat flux at the surface f the Sun.

In order to obtain the fraction of the radiative flux emitted by the Sun and intercepted by Mars, we need to relate this to the front surface exposed by Mars, i.e., a circle surface whose radius is
`r_(Mars)`,

`A_(exposed)=\pi r_(Mars)^2`

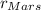So the fraction may be expressed as follows:

`(A_(exposed, Mars))/(A_(heatflux))=(\pi r_(Mars)^2)/((r_(Sun-Mars))^2)`

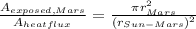
Since 1 AU =1.49598E+8 km, the resulting value is 6.9824931E-10 (the fraction of radiative flux emitted by the Sun and reaching Mars).

For the Eart,
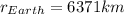`r_(Earth) = 6371 km`, applying the same formula, with r = 1 UA: 5.69788E-9