Question

What is the positive solution to the equation 0 = –x2 + 2x + 1? Quadratic formula: x = StartFraction negative b plus or minus StartRoot b squared minus 4 a c EndRoot Over 2 a EndFraction –2 + StartRoot 2 EndRoot 2 – StartRoot 2 EndRoot 1 + StartRoot 2 EndRoot –1 + StartRoot 2 EndRoot

Answer 1

C on edge

Explanation:

Just took the test!

Answer 2

`1+√(2)`

Explanation:

If a quadratic equation is defined as

`ax^2+bx+c=0` .... (1)

then the quadratic formula is

`x=(-b\pm √(b^2-4ac))/(2a)`

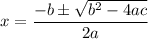
The given quadratic equation is

`0=-x^2+2x+1`

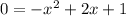
It can we written as

`-x^2+2x+1=0` .... (2)

On comparing (1) and (2) we get

`a=-1,b=2,c=1`

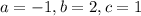
Substitute these values in the quadratic formula.

`x=(-2\pm √(2^2-4(-1)(1)))/(2(-1))`

`x=(-2\pm √(4+4))/(-2)`

`x=(-2\pm √(8))/(-2)`

`x=(-2\pm 2√(2))/(-2)`

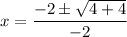
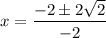
Taking out common factors.

`x=(-2(1\pm √(2)))/(-2)`

`x=1\pm √(2)`

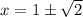
Two roots are

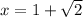`x=1+√(2)` and
`x=1-√(2)`

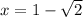
We know that

`√(2)=1.41`

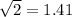
So

`1<√(2)`

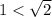
Therefore, root
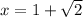`x=1+√(2)` is positive and
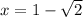`x=1-√(2)` is negative.