Answer:
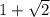
Explanation:
If a quadratic equation is defined as
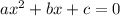 .... (1)
.... (1)
then the quadratic formula is
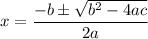
The given quadratic equation is
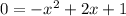
It can we written as
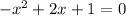 .... (2)
.... (2)
On comparing (1) and (2) we get
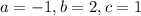
Substitute these values in the quadratic formula.
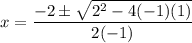
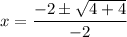
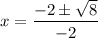
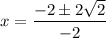
Taking out common factors.
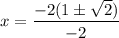
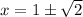
Two roots are
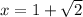 and
and
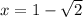
We know that
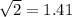
So
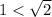
Therefore, root
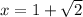 is positive and
is positive and
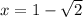 is negative.
is negative.