Question

1. A student lifts a box of books that weighs 185 N. The box is

lifted 0.800 m. How much work does the student do on the box?
2. Two students together exert a force of 825 N in pushing a
car 35 m.
a. How much work do they do on the car?
b. If the force were doubled, how much work would they do
pushing the car the same distance?
3. A 0.180-kg ball falls 2.5 m. How much work does the force of
gravity do on the ball?
4. A forklift raises a box 1.2 m doing 7.0 k) of work on it. What is
the mass of the box?
5. You and a friend each carry identical boxes to a room one floor
above you and down the hall. You choose to carry it first up the
stairs, then down the hall. Your friend carries it down the hall,
then up another stairwell. Who does more work?
Pocket
An Inclined
Constant force at an angle You've learned that a force exerted in the

Answer 1

Work is done when a force causes displacement. The student lifting the box does 148 joules of work, the two students push a car doing 28,875 joules of work, work by gravity on a ball is 4.41 joules, the mass of a box lifted by a forklift is approximately 595 kg, and both carrying methods up the stairs involve the same amount of work because they both involve the same change in height.

Step-by-step explanation:

Work & Energy Problems in Physics

Work done on an object occurs when a force causes displacement. The work (W) is calculated by the formula W = F × d × cos(θ), where F is the force applied, d is the displacement, and θ is the angle between the force and displacement direction. In the case where the force is in the same direction as the displacement, as with lifting objects vertically, the cosine factor is cos(0) which is 1, thus simplifying the formula to W = F × d.

For the problems presented:

1. The student does work of W = 185 N × 0.800 m = 148 J on the box of books.
2. The two students do work of W = 825 N × 35 m = 28,875 J on the car. If the force were doubled, the work done would be 825 N × 2 × 35 m = 57,750 J.
3. Work done by the force of gravity on the ball is W = mg × h = 0.180 kg × 9.8 m/s² × 2.5 m = 4.41 J (approx).
4. The mass of the box can be found by re-arranging the work-energy theorem: W = mgh → m = W / (g × h). Therefore, m = 7.0 kJ / (9.8 m/s² × 1.2 m) = 595 kg (approx).
5. Both parties do the same amount of work because work depends on the change in vertical position and the lifting height is the same in both cases.

Answer 2

1) 148 J

When lifting an object, the work done on the object is equal to its change in gravitational potential energy. Mathematically:

`W = \Delta U = (mg) \Delta h`

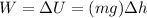
where

mg is the weight of the object

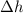`\Delta h` is the change in height

For the box in this problem,

mg = 185 N

`\Delta h = 0.800 m`

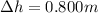
Substituting into the equation, we find:

`W=(185)(0.800)=148 J`

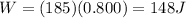
2) (a) 28875 J

The work done by a force applied parallel to the direction of motion of the object is given by

`W=Fd`

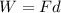
where

F is the magnitude of the force

d is the displacement

In this problem,

F = 825 N is the force applied by the two students together

d = 35 m is the displacement of the car

Substituting,

`W=(825)(35)=28875 J`

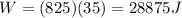
2) (b) 57750 J

As seen previously, the equation that gives the work done by the force is

`W=Fd`

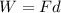
We see that the work done is proportional to the magnitude of the force: therefore, if the force is doubled, then the work done is also doubled.

The work done previously was

W = 28875 J

Now the force is doubled, so the new work done will be

`W' = 2(28875)=57750 J`

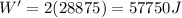
3) 4.4 J

In this case, the force acting on the ball is the force of gravity, whose magnitude is:

`F = mg`

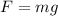
where

m = 0.180 kg is the mass of the ball

`g=9.8 m/s^2` is the acceleration of gravity

Solving the equation,

`F=(0.180)(9.8)=1.76 N`

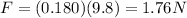
Now we find the work done by gravity using the same formula applied before:

`W=Fd`

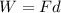
where d = 2.5 m is the displacement of the ball. We can apply this version of the formula since the force is parallel to the displacement. Substituting,

`W=(1.76)(2.5)=4.4 J`

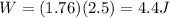
4) 595.2 kg

In this case, we have the work done on the box:

W = 7.0 kJ = 7000 J

And we also know the change in height of the box:

`\Delta h = 1.2 m`

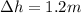
As we stated in part a), the work done on the box is equal to its change in gravitational potential energy:

`W=mg \Delta h`

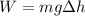
Solving for m, we find

`m=(W)/(g \Delta h)`

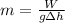
And substituting the numerical values, we find the mass of the box:

`m=(7000)/((9.8)(1.2))=595.2 kg`

5) They do the same work

In fact, the net work done by each person on the box is equal to the change in gravitational potential energy of the box:

`W=mg \Delta h`

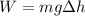
Where
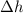`\Delta h` is the difference in height between the final position and the initial position of the box.

This means that the work done on the box depends only on its initial and final position, not on the path taken. The two men carry the box along different paths, however the reach at the end the same position, and they started from the same position: this means that the value of
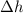`\Delta h` is the same for both of them, so the work they have done is exactly the same.