Question

Write the equation in standard form of a circle with center (-7,2), tangent to the y-axis.

Answer 1

`(x+7)^2+(y-2)^2=7^2`

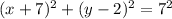
Explanation:

Tangent to y-axis means that the side of the circle TOUCHES the y axis.

Since the center is at (-7,2) and it touches the y axis, we can figure out the radius. It goes from (-7,2) to y-axis. Horizontally, the center is 7 units left of y-axis, so that is the radius ----- 7 units

The standard form of a circle is:

`(x-h)^2+(y-k)^2=r^2`

Where

(h,k) is the center

r is the radius

Putting the information into the form, we have:

`(x-h)^2+(y-k)^2=r^2\\(x-(-7))^2+(y-(2))^2=7^2\\(x+7)^2+(y-2)^2=7^2`

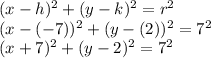
THis is the standard form.