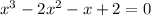Answer:
The equation of a polynomial of degree 3, with zeros 1, 2 and -1 is
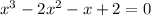
Solution:
Given, the polynomial has degree 3 and roots as 1, 2, and -1. And f(0) = 2.
We have to find the equation of the above polynomial.
We know that, general equation of 3rd degree polynomial is
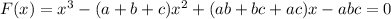
where a, b, c are roots of the polynomial.
Here in our problem, a = 1, b = 2, c = -1.
Substitute the above values in f(x)
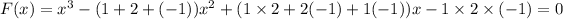
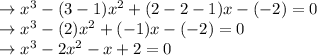
So, the equation is
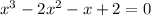
Let us put x = 0 in f(x) to check whether our answer is correct or not.
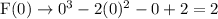
Hence, the equation of the polynomial is