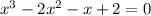Question

Write the equation of a polynomial of degree 3, with zeros 1, 2 and -1 where f(0)=2

Answer 1

The equation of a polynomial of degree 3, with zeros 1, 2 and -1 is
`x^(3)-2 x^(2)-x+2=0`

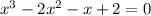
Solution:

Given, the polynomial has degree 3 and roots as 1, 2, and -1. And f(0) = 2.

We have to find the equation of the above polynomial.

We know that, general equation of 3rd degree polynomial is

`F(x)=x^(3)-(a+b+c) x^(2)+(a b+b c+a c) x-a b c=0`

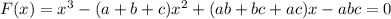
where a, b, c are roots of the polynomial.

Here in our problem, a = 1, b = 2, c = -1.

Substitute the above values in f(x)

`F(x)=x^(3)-(1+2+(-1)) x^(2)+(1 * 2+2(-1)+1(-1)) x-1 * 2 *(-1)=0`

`\begin{array}{l}{\rightarrow x^(3)-(3-1) x^(2)+(2-2-1) x-(-2)=0} \\ {\rightarrow x^(3)-(2) x^(2)+(-1) x-(-2)=0} \\ {\rightarrow x^(3)-2 x^(2)-x+2=0}\end{array}`

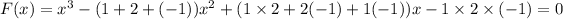
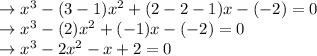
So, the equation is
`x^(3)-2 x^(2)-x+2=0`

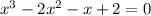
Let us put x = 0 in f(x) to check whether our answer is correct or not.

`\mathrm{F}(0) \rightarrow 0^(3)-2(0)^(2)-0+2=2`

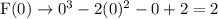
Hence, the equation of the polynomial is
`x^(3)-2 x^(2)-x+2=0`