Answer:
Maximum value of f(x) for x > 0 is 90 and the maximum value of g(x) for x > 0 is 32.
The end value for x > 0, of both the functions f(x) and g(x) is -∞.
Step-by-step explanation:
The graph of f(x) shows that it is a parabola having the vertex at (10,90) and its axis is parallel to - Y-axis and also it passes through the point (0,0) point.
Therefore, the equation of f(x) is given by
(x - 10)² = - 4a (y - 90)
If it passes through (0,0) point, then (- 10)² = -4a (-90)
⇒ a =
 =
=
 .
.
Hence, the equation becomes
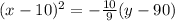
⇒
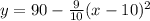 .......... (1)
.......... (1)
Now, the maximum value of f(x) for x > 0 is 90. (Answer)
Again, g(x) = x² (6 - x) ............ (2)
Hence, g'(x) = 12x - 3x² = 0 for maximum g(x) value.
⇒x = 0 or x = 4
Now, for x > 0 i.e. x = 4, g(x) = 32 is the maximum value of g(x) for x > 0. (Answer)
Now, for x approaches to +∞, then value of f(x) will approach -∞ {From equation (1)} (Answer)
And, for x approaches to +∞, then value of g(x) will approach to -∞ {From equation (2)} (Answer)