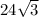Answer:
a)
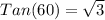
b) h = 12
c) Area =
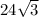
Explanation:
a)
To answer this, we need the 30-60-90 triangle.
Attached is the picture.
Since we want the value of "TAN", we need to remind ourselves, what is the ratio of TAN. By definition, TAN is the ratio of the side "OPPOSITE" to "ADJACENT".
Note: the hypotenuse is the longest side and also the side opposite of 90 degree angle. The "opposite" side is angle's direct opposite and the remaining side is "adjacent".
Since we want Tan(60), we look from 60 degree angle. We need "opposite" and "adjacent" side.
- The opposite of 60 degree angle is

- The adjacent of 60 degree angle is 1
So, the value of tan(60) is:
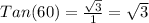
b)
We see that h is "opposite" to 60 degree angle.
We also see that
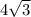 is "adjacent" to the 60 degree angle.
is "adjacent" to the 60 degree angle.
Thus, we can write:
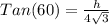
We know the value for Tan(60), we plug that in and cross multiply to find the value of h. Shown below:
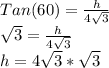
Remember to rule for surds:
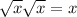
So we have:

The value of h is 12
c)
The area of a triangle is given by the formula shown below:

Where
A is area
b is the length of base
h is the height (perpendicular to base)
Looking at the triangle, the base, b, is:
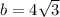
and the height, h, is
h = 12
Hence, we can calculate the area of the triangle as:
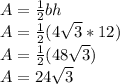
Thus this is the exact area,