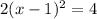Question

Which of the following reveals the minimum value for the equation 2x^2 − 4x − 2 = 0?

Answer 1

`2(x-1)^(2)=4`

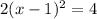
Explanation:

The options of the question are

2(x − 1)2 = 4

2(x − 1)2 = −4

2(x − 2)2 = 4

2(x − 2)2 = −4

we have

`2x^(2) -4x-2=0`

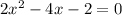
This is a vertical parabola open upward

The vertex represent the minimum value

The quadratic equation in vertex form is

`y=a(x-h)^2+k`

where

a is a coefficient

(h,k) is the vertex

so

Convert the quadratic equation in vertex form

Factor 2 leading coefficient

`2(x^(2) -2x)-2=0`

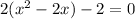
Complete the squares

`2(x^(2) -2x+1)-2-2=0`

`2(x^(2) -2x+1)-4=0`

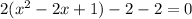
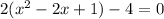
Rewrite as perfect squares

`2(x-1)^(2)-4=0`

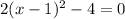
The vertex is the point (1,-4)

Move the constant to the right side

`2(x-1)^(2)=4`