Answer:
A curve is given by y=(x-a)√(x-b) for x≥b. The gradient of the curve at A is 1.
Solution:
We need to show that the gradient of the curve at A is 1
Here given that ,
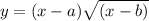 --- equation 1
--- equation 1
Also, according to question at point A (b+1,0)
So curve at point A will, put the value of x and y
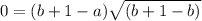
0=b+1-c --- equation 2
According to multiple rule of Differentiation,
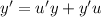
so, we get
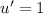
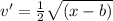
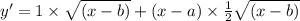
By putting value of point A and putting value of eq 2 we get

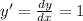
Hence proved that the gradient of the curve at A is 1.