Answer:
0.8945
Explanation:
The average life of smokers,
 is 60 months
is 60 months
Standard deviation is 8 months
Random sample, n is 30 smoke detectors

=

=
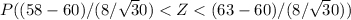
= P(-1.37 < Z < 2.05)
= P(Z < 2.05) - P(Z < -1.37) Then from the standard tables, the Z values are 0.9798 for Z=2.05 and 0.0853 for Z=-1.37
= 0.9798 - 0.0853
= 0.8945
Therefore, the probability that a random sample of 30 smoke detectors will have a lifetime between 58 months and 63 months is 0.8945