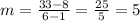Answer:
5
Explanation:
To find the average rate of change of the function between two points
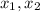 , we can use the following formula:
, we can use the following formula:
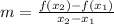
The function in this problem is
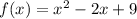
At
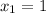 , we have
, we have
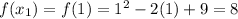
At
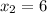 , we have
, we have
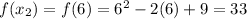
So now we can apply the first formulat to find the average rate of change of the function between the two points: