Question

The maximum displacement of an oscillatory motion is A=0.49m. Determine the position x at which the kinetic energy of the particle is half it's elastic potential energy

Answer 1

The position x, is ± 0.4 m.

Step-by-step explanation:

The total mechanical energy of the oscillatory motion is given as;

`E_T = U +K.E\\\\E_T = (1)/(2) kA^2\\\\ (1)/(2) kA^2 = U +K.E\\\\K.E = (1)/(2) kA^2 - U ----equation(1)`

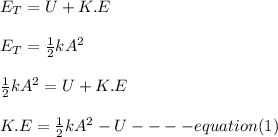
When the kinetic energy (E) is half of the elastic potential energy (U);

`K.E = (U)/(2) ----equation(2)`

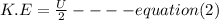
Equate (1) and (2)

`(U)/(2) = (1)/(2) kA^2 - U\\\\U = kA^2 -2U\\\\U+2U = kA^2\\\\3 U = kA^2\\\\3((1)/(2) kx^2) = kA^2\\\\(3)/(2) x^2=A^2\\\\x^2 = (2)/(3) A^2\\\\x = \sqrt{(2)/(3) A^2} \\\\x = A\sqrt{(2)/(3) } \\\\x = 0.49\sqrt{(2)/(3) }\\\\x = + /- (0.4 \ m)`

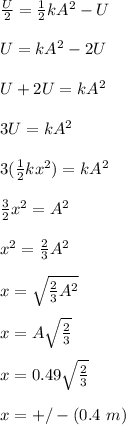
Thus, the position x, is ± 0.4 m.