Answer:
The position x, is ± 0.4 m.
Step-by-step explanation:
The total mechanical energy of the oscillatory motion is given as;
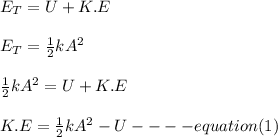
When the kinetic energy (E) is half of the elastic potential energy (U);
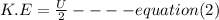
Equate (1) and (2)
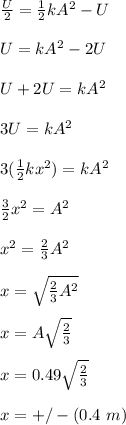
Thus, the position x, is ± 0.4 m.