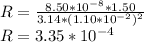Question

A 1.50-m cylinder of radius 1.10 cm is made of a complicated mixture of materials. Its resistivity depends on the distance x from the left end and obeys the formula rho(x)=a+bx2, where a and b are constants. At the left end, the resistivity is 2.25×10−8Ω⋅m, while at the right end it is 8.50×10−8Ω⋅m. What is the resistance of the rod?

Answer 1

Resistance = 3.35*
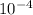`10^(-4)` Ω

Step-by-step explanation:

Since resistance R = ρ
`(L)/(A)`

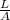
whereas
`\rho(x) = a + bx^2`

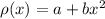
resistivity is given for two ends. At the left end resistivity is
`2.25* 10^(-8)` whereas x at the left end will be 0 as distance is zero. Thus

`2.25*10^(-8) = a + b(0)^2\\ 2.25*10^(-8) = a + 0 \\2.25*10^(-8) = a`

At the right end x will be equal to the length of the rod, so
`x = 1.50\\8.50*10^(-8) = (2.25*10^(-8)) + ( b* (1.50)^2 )\\8.50*10^(-8) - (2.25*10^(-8)) = b*2.25\\(6.25*10^(-8))/(2.25)  = b\\b = 2.77 *10^(-8)`

Thus resistance will be R = ρ
`(L)/(A)`

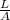
where A = π
`r^2`

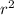
so,

`R = (8.50*10^(-8) * 1.50)/(3.14*(1.10*10^(-2))^2) \\R=3.35 * 10 ^(-4)`