The value of test static we get is - 2.24
As per given information,
Sample n = 14
Mean X 3.7
Standard deviation = σ = 0.5
Null and alternative hypotheses:
Ηο: μ > 4
Ha : μ < 4
From these we can say that it is a left-tailed test.
The test static is
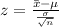
z =
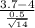
z =
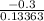
z = - 2.244994431
After rounding off the value of z is - 2.24