Question

An aircraft component is fabricated from an aluminum alloy that has a plane strain fracture toughness of 40MPa. It has been determined that fracture results at a stress of 300 MPa when the maximum (or critical) internal crack length is 4.0 mm. For this same component and alloy, will fracture occur at a stress level of 260 MPa when the maximum internal crack length is 6.0 mm? Why or why not?

Answer 1

Yes, fracture will occur

Step-by-step explanation:

Half length of internal crack will be 4mm/2=2mm=0.002m

To find the dimensionless parameter, we use critical stress crack propagation equation

`\sigma_c=\frac {K}{Y \sqrt {a\pi}}` and making Y the subject

`Y=\frac {K}{\sigma_c \sqrt {a\pi}}`

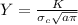
Where Y is the dimensionless parameter, a is half length of crack, K is plane strain fracture toughness,
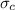`\sigma_c` is critical stress required for initiating crack propagation. Substituting the figures given in question we obtain

`Y=\frac {K}{\sigma_c \sqrt {a\pi}}= \frac {40}{300\sqrt {(0.002*\pi)}}=1.682`

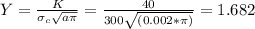
When the maximum internal crack length is 6mm, half the length of internal crack is 6mm/2=3mm=0.003m

`\sigma_c=\frac {K}{Y \sqrt {a\pi}}` and making K the subject

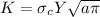`K=\sigma_c Y \sqrt {a\pi}` and substituting 260 MPa for
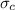`\sigma_c` while a is taken as 0.003m and Y is already known

`K=260*1.682*\sqrt {0.003*\pi}=42.455 Mpa`

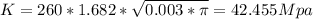
Therefore, fracture toughness at critical stress when maximum internal crack is 6mm is 42.455 Mpa and since it’s greater than 40 Mpa, fracture occurs to the material