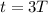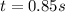Answer:
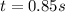
Step-by-step explanation:
As we know that the block of wood is suspended by spring
Now at equilibrium position we have net force balanced on it
so we have

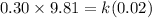
so we will have
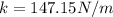
now the time period of the spring block system for one complete oscillation is given as
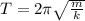
now plug in all values in it
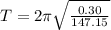
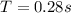
Now total time to complete 3 cycles is given as