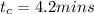Question

An asphalt pavement drains into a rectangular concrete channel. The catchment surface has an average slope of 1.0%, and the distance from the catchment boundary to the drain is 30 m. The drainage channel is 60 m long, 20 cm wide, and 25 cm deep, and has a slope of 0.6%. For an effective rainfall rate of 50 mm/h, the flowrate in the channel is estimated to be 0.02 m3 /s. The Manning n for an asphalt surface is 0.011 and for a concrete surface is 0.013. Estimate the time of concentration of overland flow for the catchment. (Hint: Use the kinematic-wave equation for overland flow.)

Answer 1

`t_(c)=4.2 mins`

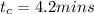
Explanation:

Using kinematic-wave equation to calculate the time of concentration

`t_(1)=\frac {6.99}{i_(e)^{(2)/(5)}}(\frac {nL}{\sqrt {S_(o)}})^{\frac {3}{5}}`

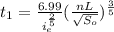
Where
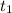`t_(1)` is time of concentration in minutes, n is Manning’s roughness coefficient, L is travel distance between catchment boundary and drain in metres,
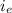`i_(e)` is effective rainfall intensity in mm/h,
`S_(o)` is the slope of the ground

Substituting L with 30 m as given,
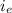`i_(e)` with 50 mm/h as provided,
`S_(o)` with 0.01 as given, Manning’s coefficient with 0.011 as given then

`t_(1)=\frac {6.99}{(50 mm/h)^{(2)/(5)}}*(\frac {0.011*30}{\sqrt {0.01}})^{\frac {3}{5}}`

`t_(1)=\frac {6.99}{4.78}(\frac {0.33}{0.1})^{\frac {3}{5}}`

`t_(1)=3 mins`

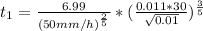
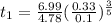
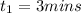
The area, A of rectangular channel in terms of channel depth

A=wd where d is depth and w is channel width

Substituting w with 20cm which is 0.2m

A=0.2d

Wetted perimeter of rectangular channel

P=2d+w=20d+0.2

From Manning’s equation of flow

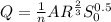`Q=\frac {1}{n}AR^{\frac {2}{3}}S_(0)^(0.5)` where q is flow rate, A is cross-sectionall area, R is hydraulic radius,
`S_(o)` is the slope and n is Manning’s coefficient

The flow rate, q is given in the question as 0.02 m3/s and Manning’s coefficient for overland flow which corresponds to concrete is given as 0.013

`0.02\frac {m^(3)}{sec}=\frac {1}{0.013}* \frac {(0.2d)^{\frac {5}{3}* (0.006)^(0.5)}}{(2d+0.2)^{\frac {2}{3}}}`

`1=\frac {1}{0.013*0.02\frac {m^(3)}{sec}}* \frac {(0.2d)^{\frac {5}{3}* (0.006)^(0.5)}}{(2d+0.2)^{\frac {2}{3}}}`

`1=\frac {(0.006)^(0.5)}{0.013*0.02}* \frac {(0.2d)^{\frac {5}{3}}}{(2d+0.2)^{\frac {2}{3}}}`

`1=297.92*\frac {(0.2d)^{\frac {5}{3}}}{(2d+0.2)^{\frac {2}{3}}}`

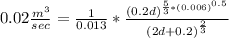
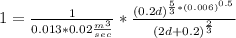
d=0.12m

We can now get the flow area which we already stated is 0.2d and now we have d

`A=0.2*0.12=0.024 m^(2)`

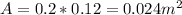
To find the velocity of flow in the drainage channel, we divide discharge by velocity hence

`V_(channel)=\frac {Q_(channel)}{A}`

`V_(channel)=\frac {0.02}{0.024}=0.83 m/s`

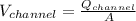
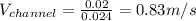
The time of concentration in the catchment area,
`t_(2)`

`t_(2)=\frac {60}{0.83}=72.3 sec=72.3/60=1.2 mins`

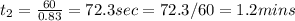
Total time of concentration,
`t_(c) =t_(1)+t_(2)=3+1.2=4.2 mins`

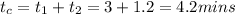
Therefore,
`t_(c)=4.2 mins`